Метод интервалов – одна из немногих тем,
которая не требует предварительной теоретической подготовки, ибо аналогичная
задача была поставлена при изучении темы «квадратные неравенств». Разница
только в том, что параболу легко построить по ее нулям, а для графика функций,
состоящих из трех и более скобок, требуются дополнительные исследования.
Фактически учителю достаточно поставить
перед учеником задачу поиска промежутков знакопостоянства левой части. Если
ученик не понимает смысла данного термина – нужно вернуться назад к свойствам
функций и квадратным неравенствам.
Как известно, перед тем как определять
поведение графика на промежутках необходимо найти границы промежутков
знакопостоянства. Они могут быть или нулями функции, или точками, в которых
значений не существует. Найдем критические точки.
Существует два
способа для расстановки знаков между найденными критическими точками:
1) Использование пробных точек в каждом промежутке.
2) Поиск знака в каком-нибудь одном из них с последующим применением законов чередования знаков на всей оси.
Второе удобнее и
практичнее, но без первого понять метод знаков чрезвычайно трудно. Не надо
ограничиваться тем, что просто сообщать ученику правило перехода через четную и
нечетную степень и просто закрепляют его на большом количестве заданий.
Действуйте иначе. Правило чередования можно
и нужно объяснять. Для этого можно
использовать самый простой пример сочетания линейных скобок (не более
трех) и сравнивает распределение их знаков в двух пробных точках соседних
промежутков. Все скобки (кроме одной) эти знаки повторят, а поменяет его та
скобка, от которой образовалась общая граница данных промежутков. На это
обстоятельство нужно обращать особое внимание учащегося. Затем нужно спросить:
«Как изменится распределение знаков в случае наличия четной степени у
рассматриваемой скобки?». Обычно на такой вопрос ученики отвечают правильно.
Подмеченная закономерность тут же
фиксируется в виде записи правила чередования: при переходе через критическую
точку, образованную от линейной скобки в нечетной степени знак на промежутке
меняется, а если степень четная – сохраняется. Пожалуй, это основной момент в
теме.
Определение знака в
правом промежутке
Чаще можно обойтись и без подстановки
пробных точек. Для этого нужно обратить внимание на особенность чисел из
правого промежутка. Если мы возмем в качестве пробной точки очень большое
число, например, 1000000, то получим в каждой скобке тот же знак, какой имеется
у коэффициента перед переменной. Если ее степень нечетная – она этот знак
сохранит. Поэтому он будет определяться произведением коэффициентов,
расположенных в скобках с нечетными степенями. Я предпочитаю оформить это
наблюдение в виде правила и записать в теоретическую тетрадь. Хватит следующего
комментария: «Модуль числа из правого промежутка настолько велик, что в
независимости от свободного слагаемого линейной скобки ее знак совпадет с
коэффициентом при иксе». Поэтому мы смотрим только на знаки старших
коэффициентов и подписываем их над каждой скобкой для финального учета.
Советы по оформлению
решений
Отработка моторики
действий по выполнению любого математического алгоритма – чрезвычайно важный
этап в работе с учеником (особенно с не самым сильным). В методе интервалов
есть несколько формальных моментов, о которых нужно предупреждать ученика и
которые желательно соблюдать:
1) При переносе критических точек на рисунок сначала надо пересчитать их количество, затем равномерно распределить по числовой оси, а уже потом прикреплять к ним числа в порядке возрастания. Как часто бывает? Ученик отмечает первую же попавшую ему на глаза критическую точку посередине оси, затем еще одну. После этого выясняется, что третья точка находится между двумя предыдущими, а четвертая между третьей и второй и так далее. В результате информация концентрируются в середине рисунка, и он теряет разборчивость. Приходится переделывать заново.
1) При переносе критических точек на рисунок сначала надо пересчитать их количество, затем равномерно распределить по числовой оси, а уже потом прикреплять к ним числа в порядке возрастания. Как часто бывает? Ученик отмечает первую же попавшую ему на глаза критическую точку посередине оси, затем еще одну. После этого выясняется, что третья точка находится между двумя предыдущими, а четвертая между третьей и второй и так далее. В результате информация концентрируются в середине рисунка, и он теряет разборчивость. Приходится переделывать заново.
Инструкция с
поэтапным переносом точек позволяет снижать вероятность не только появления
скопления знаков в узкой части рисунка, но и избегать ошибок при расстановке и
сравнении. Почему? Потому, что является возможность организовать
последовательный перенос точек, от наименьшей до наибольшей. Каждая следующая
сравнивается только с предыдущей (в соответствии с порядком возрастания или
убывания). Для того, чтобы не пропустить какую-либо из них и быстрее сравнить
оставшиеся границы будущих промежутков вычеркивайте отмеченные точки из списка
таким образом:
В таком же ключе можно рекомендовать ученику отмечать точки.
2) Знаки на промежутках должны располагаться по другую сторону от прямой (в верхней ее части), а критические точки подписываться по другую сторону (в нижней).
3) Тем самым мы расчищаем рисунок и делаем его более читабельным. Для того, чтобы интервальные знаки не тонули в общей картине их желательно рисовать жирными и длинными.
О выделении
промежутков
В учебниках
математики при оформлении решений методом интервалов часто можно встретить
загадочные бугорки — кружева, расположенные над промежутками вдоль всей
оси.
Как и любой другой
знак, поставленный учителем, он должен быть объяснен ученику. Линии не несут
никакой смысловой нагрузки, а только выделяют промежутки для того, чтобы они не
утонули в потоке пробных точек (изображенных вместе с критическими). Если учитель
по математике отказывается от их использования, то и выделять ничего не нужно.
Это является дополнительным аргумент в пользу применения правила чередования
знаков. Линиями лучше всего выделять сам ответ.
О выделении
критических точек
Нули числителя, как известно, отмечаются согласно знаку неравенства (закрашиваются в случае нестрого знака и выкалываются в случае строгого), а нули знаменателя всегда отмечаются пустыми. Для того, чтобы в голове ученика это обстоятельство надежно отложилось, учителю по математике следует принять определенные правила оформления записей. Под начальным неравенством проводится вертикальная линия. Слева от нее учитель по математике записывает нули числителя, а справа нули знаменателя. Рядом с каждой колонкой можно указать характер переноса точек на рисунок. Я обычно рисую закрашенную точку у входящих в ответ нулей числителя и пустую точку рядом со списком нулей знаменателя.
Нули числителя, как известно, отмечаются согласно знаку неравенства (закрашиваются в случае нестрого знака и выкалываются в случае строгого), а нули знаменателя всегда отмечаются пустыми. Для того, чтобы в голове ученика это обстоятельство надежно отложилось, учителю по математике следует принять определенные правила оформления записей. Под начальным неравенством проводится вертикальная линия. Слева от нее учитель по математике записывает нули числителя, а справа нули знаменателя. Рядом с каждой колонкой можно указать характер переноса точек на рисунок. Я обычно рисую закрашенную точку у входящих в ответ нулей числителя и пустую точку рядом со списком нулей знаменателя.
О типичных ошибках
учеников
Условия применимости метода интервалов
должны отработаны учителем по математике особым образом. Наиболее
распространенной ошибкой учащихся в данной теме является использование
алгоритма при отсутствии нуля в правой части. Нужно предложить отдельные
задания на выявление подобных случаев. Кроме правого нуля выражение в левой
части должно быть представлено в виде произведения линейных скобок. У дробей
числитель и знаменатель должны быть также разложены на множители. За усвоением
этих моментов учитель по математике обязан следить самым пристальным образом.
Кроме ошибок, связанных с условиями применимости метода интервалов, к типичным
промахам относится пропуск нулевой критической точки. Она образуется от
множителей вида  .
.
Как далеко учитель
по математике углубляется в метод интервалов?
Cуществуют множество ситуаций,
которые сводятся к рассматриваемому методу. Одних только алгебраических случаев
насчитывается почти с десяток. Это целые и дробные левые частьи, различные
комбинации степеней и разложений, совпадения критических точек и сокращения
дробей, невозможность разложения скобок на линейные, множители — модули.
Если учитель нацелен дать сильному ученику полноценную подготовку к ЕГЭ по
математике, он должен рассмотреть все виды задач. Для логарифмических и
показательных неравенств очень актуален расширенный метод интервалов.По материалам А.Н. Колпакова, репетитора по математике. Москва
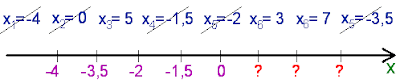

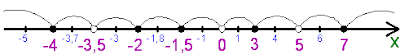
Комментариев нет:
Отправить комментарий